Kelas 7 - BAB 3 Persamaan Garis Lurus

Gambar di bawah merupakan berbagai bentuk garis lurus beserta cara menyatakan persamaan garis lurus.

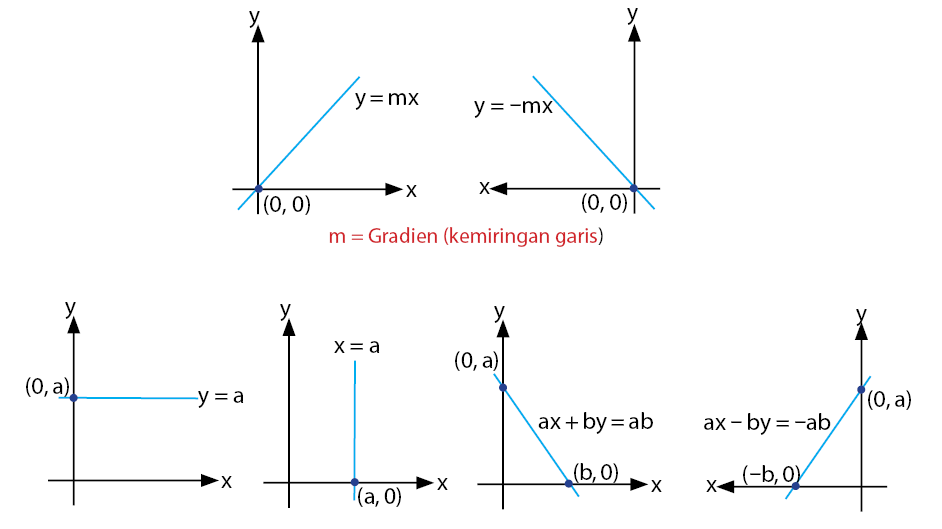
Bentuk umum persamaan garis lurus dinyatakan dalam persamaan y = mx + c, dengan m adalah gradien, x merupakan variabel, dan c adalah konstanta.

Kita akan memulai ulasan materi persamaan garis lurus dengan pengertian dan definisi gradien.

Gradien

Salah satu bagian penting dari persamaan garis lurus adalah gradien. Gradien adalah nilai yang menyatakan kemiringan suatu garis. Secara umum, nilai gradien dari suatu persamaan garis lurus dinyatakan melalui perbandingan $\frac{\Delta y}{\Delta x}$ . Biasanya, gradien disimbolkan dengan huruf m.

Perhatikan cara menentukan gradien yang diberikan pada gambar di bawah.

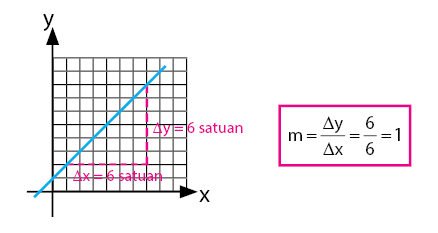
Cara menentukan gradien suatu garis lurus pada bidang kartesius juga dipengaruhi oleh arah kemiringan garis tersebut. Simak lebih lanjut cara menentukan gradien garis pada pembahasan di bawah.

Gradien Garis pada Bidang Cartesius

Garis Condong ke Kiri

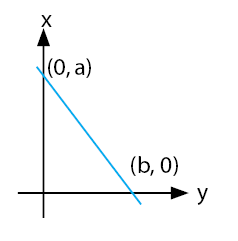
Nilai gradien gambar di atas dapat dinyatakan dalam persamaan di bawah.

$m = - \frac{a}{b}$

Garis Condong ke Kanan

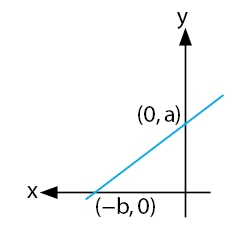
Nilai gradien gambar di atas dapat dinyatakan dalam persamaan di bawah.

$m = \frac{a}{b}$

Selain cara menentukan gradien pada bidang kartesius, gradien juga dapat dicari dari dua titik yang telah diketahui.

Gradien Garis yang Melalui Dua Titik $A(x_{1}, y_{1})$ dan $B(x_{2}, y_{2})$

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

atau

$m = \frac{y_{1} - y_{2}}{x_{1} - x_{2}}$

Selanjutnya adalah cara menentukan gradien berdasarkan persamaan garis lurus yang diketahui.

Gradien Garis dengan Persamaan ax + by + c = 0
Nilai gradien dapat diperoleh dari persamaan

$m = - \frac{a}{b}$

Posisi Antara Dua Garis

Posisi antara dua garis dibedakan menjadi dua yaitu sejajar dan tegak lurus. Dua posisi ini memiliki persamaan garis lurus yang saling berhubungan. Sehingga, jika satu persamaan garis lurus diketahu, maka persamaan garis lurus yang saling sejajar atau tegak lurus dengan garis tersebut juga dapat diketahu.

Persamaan garis lurus tersebut mempunyai syarat hubungan gradien. Syarat gradien dan gambar posisi antara dua garis lurus akan diberikan pada ulasan di bawah.

Garis yang Saling Sejajar
Garis sejajar merupakan dua buah garis yang tidak pernah akan mempunyai titik potong. Dua garis yang saling sejajar memiliki gradien yang sama.

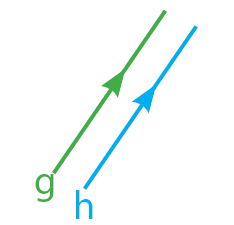garis g sejajar garis h (g // h)

Diketahui gradien garis $g = m_{g}$ dan gradien garis $h = m_{h}$ , hubungan antara gradien dua persamaan garis tersebut dinyatakan dalam persamaan di bawah.

$m_{g} = m_{h}$

Garis yang Saling Tegak Lurus
Gradien dari dua garis yang saling tegak lurus juga memiliki hubungan. Hubungannya dinyatakan bahwa gradien garis kedua merupkan lawan kebalikan dari gradien garis pertama. Atau dengan kata lainnya dapat dinyatakan bahwa hasil perkalian dua gradien tersebut sama dengan $-1$ . Misalkan gradien garis pertama memiliki nilai $m_{1} = 2$ maka nilai dari gradien garis ke dua adalah $m_{2} = - \frac{1}{2}$ . Untuk lebih jelasnya perhatikan gambar dan penjelasan di bawah.

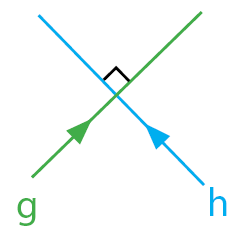garis g tegak lurus garis h

Diketahui gradien garis $g = m_{g}$ dan gradien garis $h = m_{h}$ hubungan antara gradien dua persamaan garis tersebut dinyatakan dalam persamaan di bawah.

$m_{g} \times m_{h} = -1$

Persamaan Garis Lurus

Sebuah garis lurus dapat diketahui persamannya melalui rumus dan sedikit perhitungan. Ada dua tipe soal persamaan garis lurus yang diberikan di tingkat SMP. Tipe pertama, soal yang diketahui gradien dan satu titik potong. Sedangkan tipe yang kedua adalah persamaan yang diketahui dua titik potong. Rumus untuk mencari persamaan garis itu adalah sebagai berikut.

Ada dua rumus yang dapat digunkan untuk menentukan persamaan garis lurus. Penggunaan rumusnya bergantung pada apa yang diketahui di soal. Simak kedua rumus tersebut pada pembahasan di bawah.

Persamaan garis yang bergradien m dan melalui titik $A(x_{1}, y_{1})$
$y - y_{1} = m(x - x_{1})$

Persamaan garis yang melalui titik $A(x_{1}, y_{1})$ dan $B(x_{2}, y_{2})$ .
$\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2}-x_{1}}$

Contoh Soal dan Pembahasan

Contoh Soal Aplikasi Gradien (SOAL UN Matematika SMP 2016)
Perhatikan gambar berikut!

Sebuah tangga bersandar pada dinding tembok (seperti pada gambar). Kemiringan tangga terhadap dinding tembok adalah ….

$\textrm{A.} \; \; \; \; \; \; \; \frac{4}{3}$

$\textrm{B.} \; \; \; \; \; \; \; \frac{5}{4}$

$\textrm{C.} \; \; \; \; \; \; \; \frac{4}{5}$

$\textrm{D.} \; \; \; \; \; \; \; \frac{3}{4}$

Pembahasan:
Untuk menentukan kemiringan tangga tersebut, kita perlu mencari tinggi tembok terlebih dahulu. Gunakan teorema Pythagoras untuk mencari tinggi tembok.

$t_{tembok} = \sqrt{10^{2} - 6^{2}}$

$t_{tembok} = \sqrt{100 - 36}$

$t_{tembok} = \sqrt{64} = 8 \; m$

Kemiringan dalam garis lurus merupakan gradien. Jadi, untuk mencari kemiringan tangga terhadap dinding
tembok dapat diperoleh menggunakan rumus gradien.

Pembahasan Soal UN Matematika SMP

Karena garis condong ke kanan, maka nilai gradiennya akan positif.

$m = \frac{8}{6} = \frac{4}{3}$

Jawaban: A

Contoh soal persamaan garis lurus
Persamaan garis lurus yang sejajar dengan garis $y = \frac{1}{2}x + 5$ dan melalui titik $P(-1, 2)$ ….

$\textrm{A.} \; \; \; \; \; \; \; x + 2y - 5 = 0$

$\textrm{B.} \; \; \; \; \; \; \; x - 2y - 5 = 0$

$\textrm{C.} \; \; \; \; \; \; \; x - 2y + 5 = 0$

$\textrm{D.} \; \; \; \; \; \; \; x + 2y + 5 = 0$

Pembahasan:
Persamaan garis $y = \frac{1}{2}x + 5$ memiliki gradien $m_{1} = \frac{1}{2}$ .
Karena persamaan garis baru yang akan dicari sejajar dengan garis $y = \frac{1}{2}x + 5$ maka $m_{2} = m_{1} = \frac{1}{2}$ .