Kelas 11 - Induksi Matematika

Kelas 11 - Induksi Matematika

on December 14, 2018

Jenis Induksi Matematika

Deret Bilangan

Sebagai ilustrasi dibuktikan secara induksi matematika bahwa 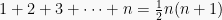$1 + 2 + 3 + \cdots + n = \frac{1}{2}n(n + 1)$ .

Langkah 1

untuk n = 1, maka :

$1 = \frac{1}{2}n(n + 1)$

$1 = \frac{1}{2}(1)(1 + 1)$

1 = 1

Bentuk untuk n = 1 rumus tersebut benar.

Langkah 2

Misal rumus benar untuk n = k, maka:

$1 + 2 + 3 + \cdots + k = \frac{1}{2}k(k + 1)$

Langkah 3

Akan dibuktikan bahwa rumus benar untuk n = k + 1. Sehingga:

$1 + 2 + 3 + \cdots + k + (k + 1) = \frac{1}{2} (k + 1)((k + 1) + 1)$

Pembuktiannya:

$1 + 2 + 3 + \cdots + k + (k + 1) = \frac{1}{2} k(k + 1) + (k + 1)$ (dalam langkah 2, kedua ruas

ditambah k + 1)

$= \frac{1}{2}k (k + 1) +\frac{1}{2} [2(k + 1)]$ . (k + 1) dimodifikasi menyerupai $\frac{1}{2} k (k + 1)$ )

$= \frac{1}{2}[k(k + 1) + 2(k + 1)]$ (penyederhanaan)

$= \frac{1}{2}(k^2 + k + 2k + 2)$

$= \frac{1}{2}(k^2 + 3k + 2)$

$1 + 2 + 3 + \cdots + k + (k + 1) = \frac{1}{2} (k + 1)(k + 2)$ (terbukti)

Bilangan bulat hasil pembagian

Suatu bilangan dikatakan habis dibagi jika hasil pembagian tersebut adalah bilangan bulat. Sebagai ilustrasi, dibuktikan secara induksi matematika bahwa 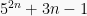$5^{2n} + 3n - 1$ habis dibagi 9.

Langkah 1

untuk n = 1, maka:

$5^{2n} + 3n - 1 = 5^{2(1)} + 3(1) - 1$

$=5^2 + 3 - 1$

= 27

27 habis dibagi 9, maka n = 1 benar.

Langkah 2

Misal rumus benar untuk n = k, maka :

$5^{2n} + 3n -1 \overset {menjadi}{\rightarrow} 5^{2k} + 3k - 1$ (habis dibagi 9)

$5^{2k} + 3k - 1 =9b$ (b merupakah hasil bagi $5^{2k} + 3k - 1$ oleh 9)

Langkah 3

Akan dibuktikan bahwa rumus benar untuk n = k + 1. Pembuktian:

$5^{2(k + 1)} + 3(k + 1) - 1$

$= 5^{2k + 2} + 3k + 3 - 1$

$= 5^2 (5^2k) + 3k + 3 -1$

kemudian 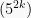$(5^{2k})$ dimodifikasi dengan memasukan $5^{2k} + 3k - 1$ .

$= 25 (5^{2k} + 3k - 1) - 75k + 25 + 3k + 3 -1$

$= 25(5^{2k} + 3k -1) - 72k + 27$

$= 25 (9b) - 72k + 27$

$= 9 (25b - 8k + 3)$ … akan habis dibagi oleh 9 (terbukti)