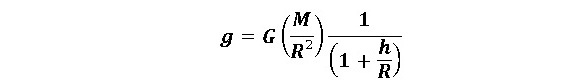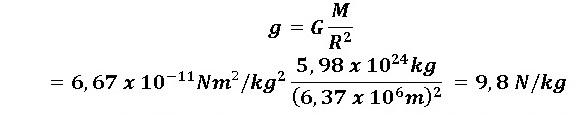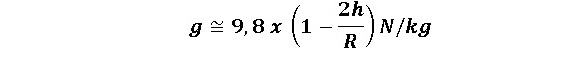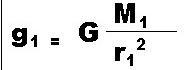- Get link
- X
- Other Apps
Untuk memahami gaya gravitasi, Newton memerhatikan memerhatikan jarak antara buah apel ke pusat bumi dan jarak bulan ke pusat bumi. Newton juga menyelidiki pengaruh massa benda terhadap gravitasi. Berdasarkan penyelidikan ini, Newton menyimpulkan bahwa suatu hukum gravitasi yaitu setiap benda dalam alam semesta selalu menarik bemda lainnya dengan gaya yang besarnya berbanding lurus dengan massa masing-masing benda dan berbanding tebalik dengan kuadrat jaraknya.
Dengan F = gaya tarik-menarik antara benda yang berinteraksi (N)
m1 danm2 = massa benda yang berinteraksi (kg)
r = jarak pusat kedua benda yang berinteraksi (m)
G = tetapan grvitasi umum (6,67 X 10-11 Nm2/kg2)
D. Gaya Tak Sentuh
Setiap benda menghasilkan medan gravitasi pada ruang di sekitarnya. Tarikan gravitasi matahari pada bumi dapat dipandang sebagai interaksi antara medan gravitasi matahari di tempat bumi berada dengan massa bumi.(Penjelasan singkat)
Arah kuat medan gravitasi selalu menuju ke pusat benda. Kuat medan gravitasi berbanding terbalik dengan jarak dari pusat benda. Tampak dari persamaan (1) dan (2) bahwa gaya yang dilakukan benda m₁ pada benda m₂ dapat ditulis sebagai
F21 = g21 m2
dengan
F₂₁ = gaya yang dilakukan benda m₁ pada benda m₂
g₂₁ = kuat medan gravitasi pada lokasi benda m₂ yang dihasilkan oleh benda m₁
m₂ = massa benda kedua
E. Medan gravitasi
Medan gravitasi merupakan sebuah vektor yang artinya, medan garvitasi memiliki arah fdan nilai. Medan gravitasi selalu dimiliki oleh setiap benda yang mempunyai massa. Setiap benda yang berada dalam suatu medan gravitasi akan saling tarik-menarik. Bentuk medan gravitasi selalu mempunyai arah garis menuju pusat benda.
Mb = massa bumi =5,97 X 1024 kgDengan g = kuat medan gravitasi (m/s2)
r = jari-jari bumi = 6,38 X 106 m
Dengan R menyatakan jari-jari bumi. Persamaan diatas dapat ditulis sebagai berikut
Jika ketinggian h jauh lebih kecil daripada jari-jari bumi, maka persamaan diats dapat didekati dengan persamaan
Kuat medan gravitasi di permukaan bumi itu sendiri adalah
Dengan demikian, kuat medan pada ketinggian h dari permukaan bumi kira-kira
Persamaan menunjukan bahwa kuat medan grvitasi atau percepatan gravitasi yang dialami oleh suatu benda bergantung pada massa bumi dan jarak benda tersebut terhadap pusat bumi, tetapi tidak bergantung pada massa benda.
Medan gravitasi pada sebuah titik yang dipengaruhi oleh lebih dari satu jumlah benda bermassa harus dijumlahkan secara vektor. Persamaan medan gravitasi pada titik P yang dipengaruhi massa M1
Sehingga besar medan gravitasi pada titik P karena pengaruh M1 dan M2
gp = √g1 + g2 +2 g1 g2 cosα
Variasi Kuat Medan Gravitasi Di Permukaan Bumi
Jika dianggap bumi benar-benar bulat dan massa jenis bumi sama di setiap titik, maka akan kita dapatkan:
- Arah medan gravitasi bumi membentuk garis lurus dan mengarah ke pusat bumi
- Pada setiap titik di permukaan bumi. Kuat medan gravitasi buminya persis sama
Namun, kenyataannya tidak demikian
- Bumi tidak bulat sempurna, tetapi agak lonjong di daerah khatulistiwa. Akibatnya, jari-jari bumi disekitar khatulistiwa lebih besar daripada jari-jari bumi disekitar kutub. Dengan demikian, kuat medan gravitasi bumi di khatulistiwa sedikit lebih kecil daripada kuat medan gravitasi bumi di sekitar kutub.
- Massa jenis bumi tidak benar-benar sama. Adanya kandungan barang tambang yang bermassa jenis besar di bawah permukaan bumi menyebabkan kuat medan gravitasi bumi pada permukaan diatasnya menjadi lebih besar. Perbedaaan kuat medan gravitasi dipermukaan bumi karena adanya deposit barang tambang dibawah permukaan bumi dimanfaatkan untuk mencari deposit barang tambang. Para peneliti mengukur kuat medan gravitasi diberbagai titik dipermukaan bumi. Berdasarkan kuat medan gravitasi yang terukur, pola perubahan, dan sebenarnya, maka dapat diprediksi adanya barang tambang, kedalaman lokasi dan jumlahnya.
- Adanya pegunungan menyebabkan benda yang ada di dekat kaki gunung ditarik kea rah pusat bumi dank e arah pusat gunung. Kedua tarikan tersebut masing-masing menghasilkan vektor kuat medan gravitasi dalam arah yang berbeda. Akibatnya, vektor kuat medan gravitasi total tidak tepat mengarah ke pusat bumi, tetapi sedikit membelok kearah pusat gunung.
F. Kuat Medan Gravitasi Di Dalam Bumi
Kita tahu semakin jauh dari permukaan bumi kuat medan gravitasi akan semakin kecil. Bagaimana jika kita masuk kedalam pusat bumi? Ternyata, ketika masuk kedalam bumi, kuat medan gravitasi makin kecil. Kebergantungan terhadap jarak dari pusat bumi mengikuti persamaan linier, yaitu
dengan
M = Massa Bumi (kg)
R = Jari-jari bumi (m)
r = Jarak dari pusat bumi (m)
G. Kehilangan Berat
Kita merasakan adanya berat pada tubuh kita karena ada 2 gaya yang bekerja sekaligus. Yang pertama adalah gaya gravitasi yang bekerja pada bumi dan bagian tubuh kita dan yang kedua adalah gaya topang oleh suatu benda misalnya lantai atau kursi tempat kita berada. Namun, bagaimana jika tidak ada gaya topang maka kita akan merasakan seolah-olah tidak memiliki berat. Kehilangan berat ini tidak berarti bahwa tidak adanya gaya gravitasi yang bekerja pada tubuh kita.
Fenomena kehilangan berat bagi para astronaut menjadi masalah yang serius karena saat mereka di luar angkasa otot dan tulang mereka tidak bekerja. Lalu saat mereka kembali ke bumi otot dan tulang yang tidak dipakai sebelumnya secara tiba-tiba menahan beban tubuh.
Untuk menghindari masalah ini, para astronaut diharuskan berolahraga saat berada di luar angkasa supaya otot dan tulang mereka tetap merasakan beban.
H. Hukum Kepler Untuk Gerak Planet
Sebelum Newton dapat menjelaskan gerak planet mengelilingi matahari, Johannes Kepler telah merumuskan hukum gerak planet yang terkenal.
Hukum I Kepler
Setiap planet bergerak mengelilingi matahari dalam lintasan berbentuk elips dan matahari terletak pada salah satu titik focus elips (elips memiliki dua titik focus)
Hukum II Kepler
Pada selang waktu yang sama, garis penghubung planet dan matahari menyapu daerah yang luasnya sama
Hukum III Kepler
Perbandingan kuadrat periode revolusi planet mengelilingi matahari dengan pangkat tiga jarak rata-rata planet ke matahari adalah sama untuk semua planet.
Pembuktian Hukum Kepler dengan Gravitasi Newton
Pembuktian Hukum II Kepler
Daerah yang disapu planet dari B ke C sama luasnya dengan daerah yang disapu dari F ke A maupun E ke D, gerak planet ini dilakukan dalam selang waktu yang sama.
Luas daerah yang disapu oleh jari-jari planet dapat ditulis sebagai
Satu planet luat daerah yang disapu berbanding lurus dengan waktu. Pada selang waktu yang sama, luas daerah yang disapu garis hubung planet dengan matahari selalu sama.
Pembuktian Hukum III Kepler
Untuk membuktikannya, kita perlu menganggap lintasan planet sekitar matahari itu lingkaran. Ini tidak terlalu salah walaupun lintasan sebenarnya berbentuk elips namun bentuknya sangat mendekati lingkaran.
Ruas kanan hanya bergantung pada massa matahari. Jadi, T² dan r³ selalu sama untuk semua planet sesuai dengan Hukum III Kepler. Dengan memasukkan nilai massa matahari M dan konstanta gravitasi universal G, maka nilai di euaskanan adalah 2,97 x 10⁻¹⁹ s²m⁻³.
I. Manfaat gravitasi
Gravitasi memungkinkan kita untuk melakukan banyak hal di dunia ini, seperti berjalan, bekerja , dan keseharian lainnya. Penerapan hukum graviatsi akan banyak kita jumpai dalam berbagai macam teknologi, karena manfaatnya yang sangat menguntungkan.
(-) Pesawat antariksa dan astronaut
Pesawat antariksa membutuhkan kecepatan yang besar untuk dapat melawan gravitasi, untuk lolos dari permukaan bumi, pesawat membutuhkan percepatan sekitar 15 kali percepatan gravitasi bumi. Dengan percepatan yang begitu besar maka astronaut akan mengalim gaya dorong oleh kursi sehingga ia akan mersakan 16 kali dari beratnya.
(-) Satelit
Agar satelit berda tetap di luar angkasa dan tidak lepas menjauh dibutuhkan gaya gravitasi bumi untuk tetap menjaganya dalm orbit tertentu, salah satu contohnya adalah satelit palapa. Teknologi GPS juga membutuhkan bantuan dari satelit-satelit yang mengorbit di bumi
- Get link
- X
- Other Apps