- Get link
- X
- Other Apps
A. Tentang Sudut
Sudut adalah pertemuan atau perpotongan 2 buah garis/sinar atau bangun yang dibentuk oleh dua garis yang yang berpotongan di sekitar titik potongnya.
Untuk ukuran sudut, kita mengenal ada beberapa macam, yaitu: derajat, radian, gone/grade.
Perhatikan ilustrasi berikut
Selanjutnya yang sering dikenalkan adalah sudut dalam ukuran derajat dan radian.
Sebagai catatan:
Ukuran derajat yang diubah ke menit atau detik yang selanjutnya disebut dengan sistem seksagesimal, yaitu:
1 derajat = 60 menit = 3600 detik, atau
1. 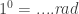 .
.
2. 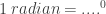
3. Jadikanlah sudut  dalam seksagesimal!
dalam seksagesimal!
4. Jadikanlah sudut 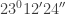 dalam satuan derajat!
dalam satuan derajat!
Jawab:
1. Perhatikanlah
Kadang dituliskan untuk 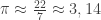 , tinggal kita masukkan saja sebagai ganti pi di atas.
, tinggal kita masukkan saja sebagai ganti pi di atas.
2. Dengan cara mirip dengan no.1, yaitu
3. Kita ingin menjadikan sudut dari ukuran derajat yang mengandung desimal ke seksagesimal.
Perhatikan langkahnya
4. Dengan cara yang kurang lebih sama, yaitu
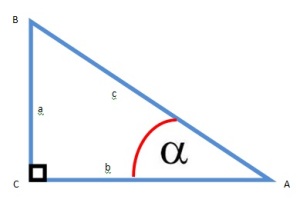
B. Perbandingan Sudut dalam Segitiga Siku-Siku
Perhatikanlah ilustrasi berikut ini
Untuk Perbandingan Sudut istimewa amati tabel berikut, khususnya sudut  .
.
Karena pada segitiga siku-siku berlaku teorema Pythagoras, maka ada baiknya kita ingat-ingat tripel Pythagoras di sini yang sering digunakan/dimunculkan .
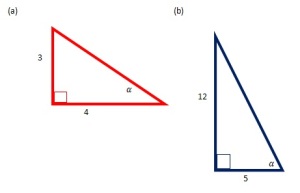
1. Tentukanlah nilai perbandingan  untuk segitiga berikut
untuk segitiga berikut
Jawab:
(a) Untuk sisi miringnya adalah
(b) Dengan langkah sebagaimana pada langkah (a), kita mendapatkan
2. Hitunglah nilai dari
Jawab:
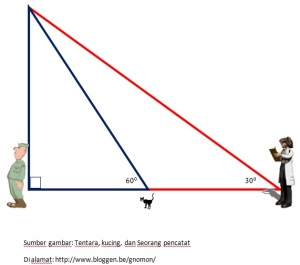
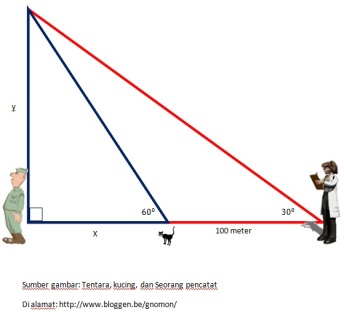
3. Perhatikan ilustrasi berikut
Jika Jarak antara kucing seorang pencatat dan kucing adalah 100 m, maka jarak Pencatat tersebut dengan seorang tentara sebagaimana gambar tersebut di atas adalah?
Jawab:
Perhatikan gambar di atas dengan diberikan tambahan keterangan sebagai berikut
Ditanya berpakah panjang jarak 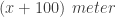 ?
?
Jadi  meter.
meter.
4. Tentukanlah perbandingan trigonometri  jika
jika 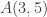 .
.
Jawab:
Perhatikan ilustrasi berikut
Dengan memandang ilustrasi gambar di atas kita mendapatkan  , dengan menggunakan teorema pythagoras kita mendapatkan
, dengan menggunakan teorema pythagoras kita mendapatkan
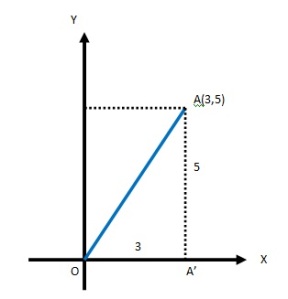
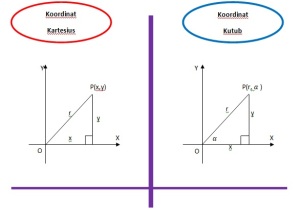
C. Koordinat Kartesius dan Koordinat Kutub/Polar
Perhatikanlah ilustrasi berikut
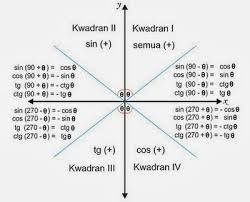
D. Perbandingan Trigonometri di Berbagai Kuadran
Perhatikan ilustrasi berikut
[Sumber]
Untuk sudut  .
.
Perbandingan trigonometri untuk sudut negatif
1. Tanpa menggunakan tabel/kalkulator tentukanlah nilai  jika diketahui
jika diketahui  .
.
Jawab:
2. Tunjukkan bahwa
Jawab:
3. Diketahui koordinat kutub titik M adalah 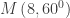 , maka koordinat kartesiusnya adalah….
, maka koordinat kartesiusnya adalah….
Jawab:
E. Identitas Trigonometri
F. Fungsi Trigonometri
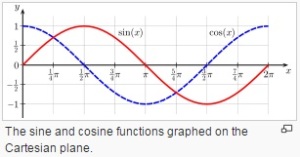
Perhatikanlah ilustrasi gambar berikut untuk grafik fungsi sinus dan cosinus
[Sumber]
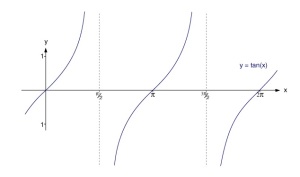
Untuk fungsi tangen,
[sumber]
Fungsi Sinus , f(x)= sin x
Fungsi Cosinus , f(x)=cos x
Fungsi Tangen , f(x)=tan x
Untuk :
G. Persamaan Trigonometri Sederhana
1. Buktikan bahwa 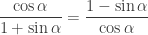 .
.
Bukti:
2. Tentukanlah himpunan penyelesaian dari persamaan  .
.
Jawab:
Jadi Himpunan penyelesaiannya adalah = 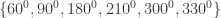 .
.
3. Lukislah grafik fungsi  .
.
Jawab:
Untuk gambar silahkan pembaca melukiskannya sendiri sebagai latihan.
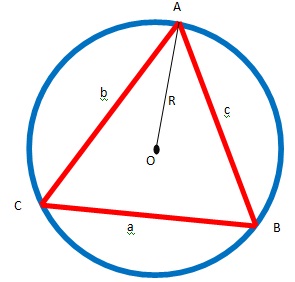
H. Aturan Sinus, Kosinus, dan Luas Segitiga
1. Aturan Sinus
2. Aturan Kosinus
3. Luas Segitiga
atau
atau
1. Diketahui  dengan panjang sisi AC=10 cm dan BC=16 cm serta luas
dengan panjang sisi AC=10 cm dan BC=16 cm serta luas  , maka besar
, maka besar  jika sudutnya lancip adalah …
jika sudutnya lancip adalah …
Jawab:
Diketahui  , maka
, maka
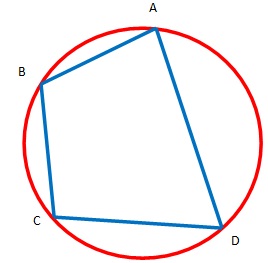
2. Perhatikanlah gambar berikut
Jika  , maka
, maka 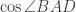 adalah ….
adalah ….
Jawab:
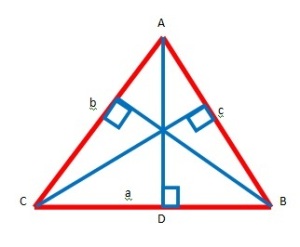
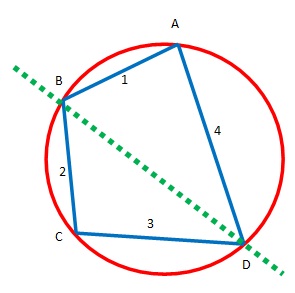
Perhatikan kembali ilustrasi berikut
Langkah awal kita gunakan garis bantu BD untuk nantinya kita mendapatkan nilai cos dari sudut A, yaitu
Selanjutnya,
3. Carilah luas  jika diketahui AB=10 cm, AC=14 cm dan BC=16 cm.
jika diketahui AB=10 cm, AC=14 cm dan BC=16 cm.
Jawab:
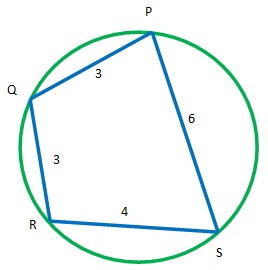
1. Perhatikanlah gambar berikut
Tentukanlah nilai  .
.
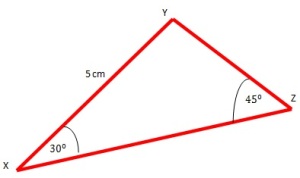
2. Perhatikanlah ilustrasi gambar berikut
Carilah besar sudut dan panjang sisi yang belum diketahui dari segitiga di atas, kemudian cari pula luasnya?
Sebuah sudut akan terbentuk dari dua buah sinar yang berpotongan. Sedangkan sinar sendiri di sini adalah sebuah garis yang berpangkal pada sebuah titik dan memanjang ke suatu arah tertentu.
Perhatikanlah ilustrasi berikut
Dari ilustrasi gambar dua sinar di atas, antara sinar  dan sinar
dan sinar  bertemu di titik O sehingga terbentuklah sudut
bertemu di titik O sehingga terbentuklah sudut  .
.
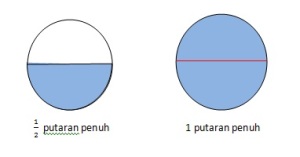
Pada materi di tingkat SMP di kenalkan ukuran sudut dalam derajat dan radian. Selanjutnya secara singkat dapat dituliskan pada satu lingkaran penuh akan terdapat 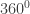 atau
atau  radian.
radian.
Coba perhatikan ilustrasi berikut!
Jika ditunjukkan dengan tabel ukuran sudutnya adalah sebagai berikut:
Sebagai catatan ukuran sudut yang diubah ke menit dan/atau detik dinamakan sebagai sistem seksagesimal, yaitu:
- Get link
- X
- Other Apps